ERNEST MOYER'S RESEARCH
Copyright, Ernest P. Moyer, Author
February, 2001
Introduction
The small antechamber located between the top of the Grand Gallery and the King's Chamber in Giza I is the most interesting of all chambers in spite of its small size. Sir Flinders Petrie, with his exquisite measurements of the Pyramid, expressed disappointment in the crudity of the construction.
See The Pyramids and Temples of Gizeh, Field and Tuer, London,1883, First Edition.
The walls, floor, and ceiling are made from mixed blocks of limestone and granite.
Refer to the discussion on page 174 and Plate XV of Our Inheritance in the
Great Pyramid, Piazzi Smyth, W. Isbister, London, 1880. The different
slabs are marked G for granite and L for limestone.
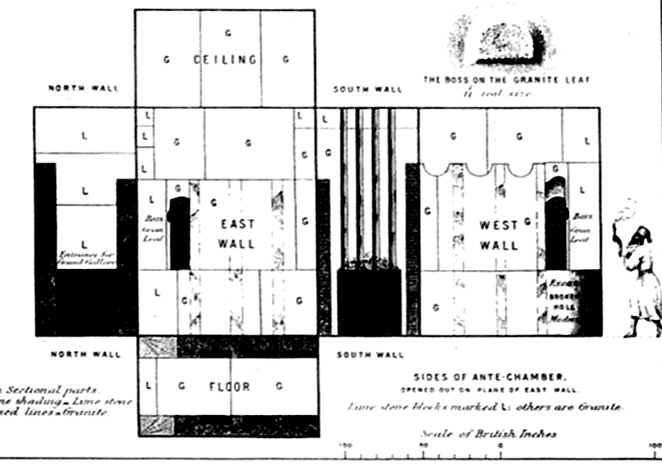 |
On the south wall above the entrance to the Kings Chamber are four grooves running vertically from the entrance to the top of the chamber. The purpose of these grooves is unknown.
Along the east and west walls are two granite linings, or wainscots, of different heights; the one on the east side is 5.0 cubits; the one on the west side is 5.42 cubits. Three grooves are cut into each granite wainscot beginning at the south end of the chamber. These grooves measure 1.0 cubits in width. At the top of each groove on the west side is a semicircular notch, as though intended for a circular beam or wooden log to be placed across the chamber. However, since no notches are cut into the grooves on the east side, any hypothetical beams would have to rest on the top. The grooves are separated from one another by a distance of about 2/7 cubits.
The thickness of the wainscots are such that the distance between them across the chamber is 2.0 cubits, the same as the width of the entrance from the Grand Gallery, and the exit to the Kings Chamber. Smyth shows the crude shape of the wainscots and narrowing of their thickness at the south wall.
A fourth groove near the north end of each wainscot does not extend completely to the floor; the rectangular bottom of the groove stops at the height of the passageway entering the antechamber from the Grand Gallery. Placed in these northern-most grooves and held in position by the granite wainscot of both sides of the chamber are two slabs of granite, one resting upon the other. The purpose of the slabs has been accepted almost universally as a design for blocking entrance to the King's chamber. How this was to be done is not known; the slabs rest solidly within their rectangular grooves.
The measurements of the granite wainscots, the grooves, and the two slabs were not reported in detail by Petrie because of their crude state.
But the dimensions of the chamber offer mathematical relationships heretofore
unrecognized.
The Dimensions of the Chamber
Following is a tabulation from Petrie's measurements. All dimensions are in the English inches he used.
48. Taking the Antechamber alone, we may say that its dimensions above the
granite wainscot of the sides, are as follows:
| Length N. to S. | ||||
| Height above floor |
2 from W. | Middle | 12 from E. | E. side |
| 147 | 116.85 | 116.22 | 116.05 | 115.65 |
| 129 | 117.00 | 116.18 | 116.03 | 115.37 |
| 114 | 117.00 | 116.11 | 115.73 | 114.07 |
| 95 | 116.55 | . . . | 115.91 | . . . |
| 70 | 116.58 | . . . | 115.93 | . . . |
| 45 | 115.91 | . . . | 116.12 | . . . |
| Breadth, E. to W. | ||||
|
Height above floor |
2 from N. | 40 from N. | 76 from N. | 2 from S. |
| 147 | 64.80 | 64.48 | 64.96 | 64.76 |
| 129 | 64.72 | 64.98 | 65.26 | 65.25 |
| 114 | 65.06 | 65.00 | 65.48 | 65.21 |
The height was measured as follows:
| Near N. wall | 14 from N. | 59 from N. | 61 from N. | S. wall | |
| At E. side | 149.47 | 149.09 | 149.17 | 149.62 | 149.63 |
| Middle | 149.53 | . . . | . . . | 149.64 | 149.64 |
| At W. side | 149.32 | 149.01 | 149.10 | 149.65 | 149.57 |
| Above gallery end |
153.04 | 152.95 | 152.83 | 152.84 | 152.61 |
From Petrie's measurements on the several pyramids he calculated that the
value of the Royal Cubit was 20.63 inches. Converting Petrie's inch
measurements to cubits, we obtain the following:
| Dimension | Range in inches | Range in Royal Cubits |
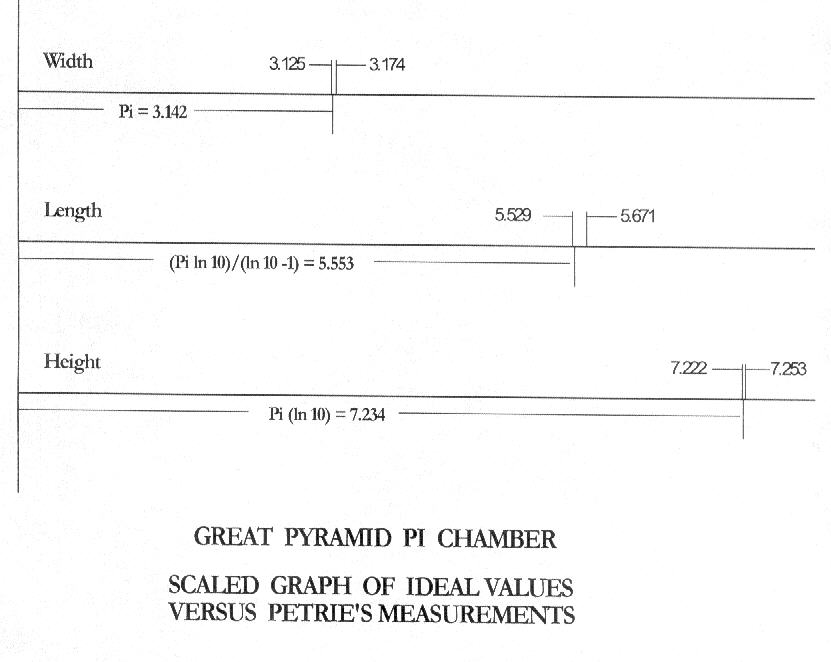
| North-to-South Length | 114.07 - 117.00 | 5.529 - 5.671 |
| East-to-West Width | 64.48 - 65.48 | 3.125 - 3.174 |
| Height | 149.01 - 149.65 | 7.222 - 7.253 |
The most obvious measurement is the width of the chamber between the east and west walls above the granite wainscots.
The width of the chamber in cubits is the numerical value of Pi.
The measurements are 3.142 cubits, +0.032 and -0.017 cubits, or error of +1.02% and -0.54%.
In this single dimension the pyramid builders demonstrated that they knew the numerical value of Pi, within the ability to control a work of stone. The dimension has withstood more than 4500 years of time, with earthquakes and the ravages of later generations.
The Height and Length Dimensions
However, the builders did not depend entirely upon this single dimension.
They designed the chamber to show knowledge of circular and spherical geometry.
Petrie reported the mean of his measurements in inches at 116.30 length, 65.00 width, and 149.35 height. In cubits these are 5.637, 3.15, and 7.239 respectively.
The relationship of the surface areas of the chamber is given by:
WL + WH = LH Equa. 1
Using Petrie's mean values we obtain
17.76 + 22.80 = 40.56 compared to 40.80 square cubits calculated directly from LH. This is a difference of 0.24, or 0.59%.
Clearly, there is an intentional design relationship among the chamber dimensions.
If we take the total chamber surface area to the surface area of a side wall we may express it by:
2WL + 2WH + 2LH = 4LH Equa. 2
Taking Petrie's mean values we obtain:
2(17.76) + 2(22.80) + 2(40.80) = 4(40.80)
or
The sum of 35.52 + 45.60 + 81.60 = 162.72 compared to 163.20 calculated directly from 4LH. This is a difference of 0.48, or 0.3% using Petrie's mean values.
This shows that the pyramid builders intended to demonstrate a relationship among all the dimensions. But what?
The meaning becomes evident when we recognize that the total surface area of the chamber is related to the surface area of one side wall by a ratio of 4:1.
162.72 divided by 40.80 = 3.988.
This differs from 4.0 by 0.012, or 0.3%, using Petrie's mean values.
This is highly intriguing for the ratio of the surface area of a sphere to the area of a circle of the same radius is also 4.0.
S = 4 X Pi X r2
The builders demonstrated knowledge of this relationship by a unique method.
The builders used rectangular geometry to represent spherical geometry.
The total chamber surface area represents the surface of the sphere; one side wall represents a circle of the same radius.
From this knowledge we can calculate the value of that radius.
r2 = LH/Pi
r2 = 40.80/3.14 = 12.987, based on Petrie's mean values.
This differs from the prime number 13.0 by 0.012 or 0.6%
If the builders intentionally chose this value it would force the relationship between L and H.
We can look at the relationship among the dimensions another way.
Equation 1 can be rearranged as follows:
1/H + 1/L = 1/W Equa. 3
This calculates as follows, using Petrie's mean values:
1/7.239 + 1/5.637 = 0.1381 + 0.1774 = 0.3155
1/Pi = 0.3183
The two numbers differ by 0.0028 or 0.88%
Thus it is possible to calculate Pi from the length and height dimensions.
This value is not obvious; it shows only in analysis of the dimensions. However, it cannot be any more accidental than the width of the chamber.
This raises the question of the mathematical degrees of freedom. If W = Pi, if HL = 40.80 to give 13.0 when dividing by Pi, and if 1/H + 1/L = 1/Pi, then all dimensions are chosen.
The conditioning values are:
LH/Pi = 13.0
Reducing Equation 3, L + H = LH/Pi.
Hence L + H = 13.0
We can see that the sum of 7.239 and 5.637 from Petrie's mean values is equal to 12.876. This differs from 13 by 0.124 or 0.96%,
Note that the builders invited our attention to the chamber dimensions by using Pi directly in one dimension. Their design conditions then led to our evaluation of the length and height dimensions, and recognition of the circular geometry. By making one dimension equal to Pi, and by making the total chamber surface area four times as great as one side wall area they tied together their knowledge of Pi as well as circular and spherical geometry.
The pyramid designers had to know the relationship between a circle, and a sphere of the same radius.
They certainly did not achieve such happy results by sheer accident.
Note that the area of the two side walls sum to the hemispherical surface area. Therefore, the north and south walls, floor and ceiling also sum to the hemispherical area.
The Logarithms of the Dimensions.
While all of this is quite astonishing, the numerical values of the chamber length and height are even more astonishing.
The mean of Petrie's height is 7.239 cubits.
This number is also unique and common to the physical sciences we practice today.
Pi (ln 10) = 7.234!
Hence,
H = Pi (ln 10)
The two values differ by less than five parts in seven thousand, or 0.07%!
"In the above expressions ln 10 means the logarithm of the number ten to the natural base e, using commonly accepted symbols and designations."
Rearranging Equation 3.
L = H X (H/Pi - 1)
If the height truly represents Pi (ln 10) then L is forced.
L = [Pi (ln 10)]/(ln 10 - 1)
(3.142 X 2.303)/(2.303 - 1) = 7.234/1.303 = 5.552.
This theoretical ideals differs from Petrie's mean of 5.637 by 0.085 or 1.5%.
These are all rather astonishing results for such a rough and crude chamber.
We can see that the builders did not use more precision in construction than
was necessary to convey their intent. Petrie may have been disappointed, but
analysis, within the errors he reported, is adequate to show that intent.
Refer to the Figure showing the dimensions to scale, and the errors reported
by Petrie. The control of the chamber dimensions was tight, in spite of the
apparent crude construction, and certainly adequate to determination of the
design.
Which Design Choice?
But now we are up against a dilemma. The L and H dimensions cannot be forced two different ways - by the number 13, and by the natural logarithmic relationship.
Taking the logarithmic relationships:
L + H = Pi (ln10) + [Pi (ln 10)]/(ln 10 - 1)
The numerical value is 12.787.
This differs from 13 by 0.213, or 1.6%.
Hence it is impossible from the construction and measurement errors to determine the builders choice, either the prime number 13, or the logarithmic relationships.
The calculated difference from Petrie's sum of the mean values to obtain 12.876 is no help in making this decision.
But we can use our heads in deciphering intent.
If I were a designer I would not want to depend upon an obscure square of the radius to demonstrate knowledge of the prime number 13. This number falls so low in the prime number regime that it is trivial. The value of 13 for the square of the circle used in the design just happens to be coincidental. The height of 7.234 cubits is crucially more important, for it directly shows knowledge of higher mathematical levels. The designer clearly used the most simple dimensions to show his intent: Pi for the width, and Pi (ln 10) for the height. (Combined with the circular and spherical relationship, the length of the chamber was then fixed.) If he had used multiples of those numbers we probably would not have detected them.
His genius lies in using cubit measures to express sophisticated mathematical knowledge.
When we discover the Pi dimension of the width, we are naturally drawn to examine the other dimensions. We might know the numerical value of Pi from more elementary mathematics, as has been known at least since Babylonian and Greek days, but the knowledge of logarithms is a recent development.
We would not recognize Pi (ln 10) unless we had a similar level of knowledge.
Stating it otherwise,
The designer of the Great Pyramid had a level of mathematical knowledge unequaled until the past three hundred years.
Furthermore, the designer was talking to us without the symbols of language. He used mathematics. Since mathematical reasoning is universal, beyond linguistic symbolism,
the designer found a way to communicate with the future where the linguistic symbolism would be unknown.
The question that naturally arises is this:
Did the designer expect his level of knowledge to become lost, and used the Great Pyramids of Egypt to make a record of his existence?
As I shall show, the answer to this question is a resounding, Yes.
All dimensions represent fundamental geometric and physical constants, recognizable by any competent modern mathematician, physicist or engineer. They are constants that derive from applied mathematics and the laws of nature. No other numbers satisfy the values so simply, so uniquely, and so closely.
Our difficulty lies in a measurement related to a mathematical base of natural numbers. There is no evidence for such knowledge until modern times. None of the preserved records of ancient Greece, Mesopotamia, or Egypt show such knowledge. How could a more ancient people possess it?
In spite of this overwhelming tradition, the values are unique. If the designers were familiar with natural number systems and they wished to express their knowledge in a work of stone they made an excellent choice for the dimensions. Pi (in 10) shows knowledge of three distinct mathematical forms: circular geometry, base ten number systems, (10), and natural base number systems, (ln).
But these results do not sit in isolation. Other dimensions provide confirmation in all four great pyramids.
Other factors are important.
Petrie noted that earthquakes had disturbed the north-south width measure of the King's chamber. The large granite ceiling beams were cracked by seismic disturbances sometime in the past. The same problem may affect this small chamber, since the greatest dimensional error is in the length along the same line as the greatest error in the King's chamber. If the side walls rest upon the floor stones, and the ceiling rests upon the side walls, we should expect the least error in the height, since seismic disturbances would not change the height if the chamber were not tightly bonded to the core masonry and was left floating in the structure, unless the earthquakes were violently severe. Evaluation of the floor levels shows the effect of seismic disturbances.
I shall not discuss those effects here, since they do not impact upon this study.
This line of thinking leads to the possibility that the granite wainscots and slabs in the antechamber have a practical purpose other than inhibiting entry to the King's chamber.
The two side linings with the stone slabs inserted between them would prevent the north and south walls from collapsing inward under seismic disturbances. Only outward shifts could occur to enlarge the chamber. The measurements show a median larger than the ideal, not smaller. This postulate may be verified by searching for space between the two wainscots and the respective walls.
However, this does not explain the other three grooves in the wainscots. Perhaps their purpose relates to other mathematical properties, or perhaps the builders changed their minds. Further observation and measurement seem necessary. If this part of the design was left in an unfinished state, shown by the different heights of the wainscots, we may never be able to determine the purpose of those parts.
In fact, the builders may have intentionally left the wainscots in an unfinished and contrasting condition to force our attention away from them, and on to the walls of the chamber.
Ernest Moyer is author of a book, "Our Celestial Visitors," in which he thoroughly examines the UFO
and abduction phenomenon, with much new material never before published. Books
may be purchased through
www.amazon.com
or directly from:
Moyer Publishing
PO Box 1206
Hanover, PA 17331
Retail prices are $22.95 for soft cover, $34.95 for hard cover. Moyer Publishing offers them at $14.00 and $21.00 respectively, plus $3.00 shipping and handling
within the United States. Foreign shipments cost more. Inquire of your Post Office for two (2)
pound shipping weight, and include additional cost in your check or money order.
Remember that checks or money orders drawn on banks outside the United States may cost more to
process than the value of the item. All funds should be in US currency.