This article focuses primarily on the e and Pi proportions present in the Great Pyramid. Because of their extreme close proximities to GP's observed ratio I have for that reason given more attention to these two ratios with less focus on two other very interesting and important ratios, namely; the historically recognized Phi proportion and the popular results oriented 'Amazing Little Epsilon' proportion. (William Kapsaris will forgive me)
I am still actively involved in an ongoing search find out whether or not the e ratio has been officially noted. So it is with trepidation that I claim to have 'discovered' it, hence as of this writing my stand on this is that I have found an interesting ratio but do not present it as original (yet). Namely given the triangle;
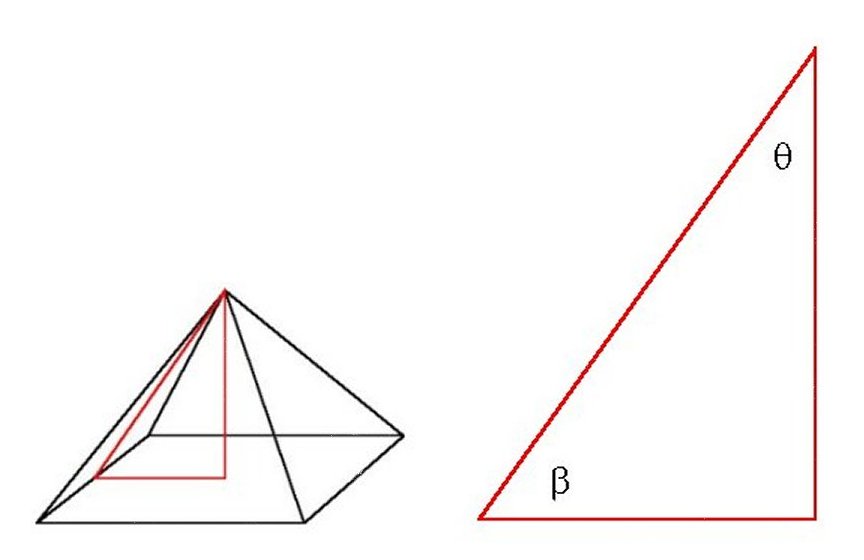
beta/theta ≈ e/2
a.k.a. The e proportion
(I say approximate here meaning 'approximate' as compared to GP angles beta and theta)
The true equivalence as derived from this equation can be found towards the bottom of this article -- for the more math minded among you.
If indeed it turns out that this ratio is known that's fine, this article then can be viewed as an attempt to garner it the recognition it undoubtedly never received. For it is surely there... quietly hidden within the Pyramids stone masonry for all of time. It remains, in my mind, as fascinating to me now as it was the day I found it. I hope if nothing else to present the reader with yet another Pyramid puzzle to ponder, another angle (pun intended) to the current views of the Great Pyramids fundamental design element, independent or maybe not so independent of the widely accepted Pi and Phi proportions. So without further ado I submit here... the e proportion.
BRIEF INTRODUCTION TO THE EULER NUMBER
2.7182818284...
The Euler number (pronounced 'oiler') goes by many names such as; epsilon, the exponential number, and Napiers number to name a few, but the name I shall refer to it as throughout this essay is also its most common name and is simply... e.
Without overwhelming you with too much detail on the history of this fascinating number I kindly defer the reader to an excellent book; 'e The Story of a Number' by Eli Maor (Princeton Press) for everything e. But let me give you just a wee bit of background on this most important of numbers that lay quietly nestled between 2 and 3. First off it is the base of the Natural Logarithms as credited to the Swiss mathematician/physicist and namesake Leonhard Euler around 1750. But it's actual date of discovery or as I like to think, re-discovery, remains shrouded in mystery.
This powerhouse of a number is used virtually in all disciplines of science and is just as important on its own merits as is Pi. The number e however, is far lesser known to the general audience because it is not as visually friendly (I'm sure you know someone like that) and is primarily algebraic and therefore more abstract. Pi on the other hand, as everyone knows, relates the circumference of a circle to its diameter and is well liked by most everyone. All right it's a dumb analogy, I know, but the point is that e is a virtual workhorse of a number and without it we wouldn't have had the industrial revolution and that means we'd likely be without thumbtacks, toothpaste, car wax, and my personal favorite, lime sherbert. The number e also has a very unique quality that resides in the realm of calculus and is one of the main reasons for its importance e.g. when the exponential series is differentiated or integrated with respect to 'x' then the resulting series is 'itself'. Does that make sense? No? Don't worry I just read that out of a book anyway and there won't be a test.
All that historians can really tell us about e's origins is that the number was hinted at around the early sixteen hundreds, and thought probably to have arisen in (as Maor puts it) 'the mundane study of compound interest'. Again, Einstein may well have hit the mark with his tongue-in-cheek statement as alluded to in the header of this article. For if it proves to be true that the Great Pyramid was (is) a machine the likes of which we have never seen, then is it really that hard to speculate that the hidden number e within its very angles could have been deliberate on the part of the designer(s)? The very presence of e in GP gives credibility to the notion that the Ancients had more knowledge indeed vastly more knowledge than traditional historians give them credit for. Unlike Pi and Phi, e's derivation requires mathematical thinking that the ancient world wasn't supposed to have possessed and that alone is worth taking note.
What splendid harmony to see three of the most important mathematical constants represented to such high degrees of accuracy within the confines of a single man-made structure and an ancient one at that! It gives me chills to consider the implications of an ancient society that had knowledge of the number e simply because it presents a whole new ballgame. I hope to present just such evidence in the course of this discussion and leave it to you the reader to decide. Okay, okay, enough boring history... now on to the good stuff!
THE FIND (440 POINTS THE WAY)
In January of 2001 while tinkering with the number 440, or somewhere there-abouts I came across an interesting numerical identity in the Great Pyramid. I found that when you double the base angle beta(β) in its primary vertical right triangle and divide by the angle theta(θ) at the apex, the result is very, very close to e. In addition to knocking my socks off this was like some kind of magical fulfillment. You see, during that time I was driven, almost to the point of obsession, to figure out why I have perfect pitch to the frequency 440Hz and none other. So, as I was examining the number 440 I noticed a couple of numbers very close to 440 that struck me as interesting;
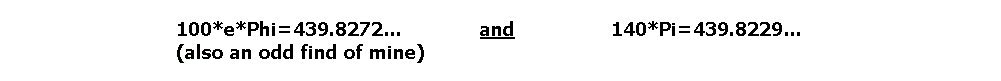
For reasons too bazaar to be explained here, I was hell-bent on finding a link between e, the GP base length of around 440 cubits, and the acoustical sound frequency of 440Hz resident in the Kings Chamber, par - Christopher Dunn 'The Giza Power Plant' (Bear and Company Publishers). I must admit to actually hoping to find some tie in to e within the angles of the Great Pyramid. And what's kind of scary is that deep inside of me I honestly think I knew I would... and I did.
Upon seeing the hidden Euler number for the first time I was in disbelief. I checked, checked and re-checked my math and sure enough it was indeed there! The feeling was fantastic! I had found what I was looking for. I remember thinking, "My God!, I've got to read up on this!" So I immediately took to the books in search of the ratio I was lucky enough to stumble upon for surely it would be strewn throughout all the GP literature. I note here that up to that point I had read very little on the esoteric nature of the Great Pyramid, only hearing stories from TV documentaries and from friends steeped in the Ancient Egyptian mysteries, so thoughts of wonder and mystery were in my mind a-plenty.
Well not only, as it turns out, have I been unsuccessful in finding so much as a remnant to this ratio by way of the internet, books, and online academic searches of peer reviewed periodicals through the paid services Infotrack and ProQuest via my local library, to my utter astonishment everyone I shared it with seemed (for the most part) indifferent and unenthusiastic from what I only guessed to be 'mathphobia'. "It's e for God sake! Why don't they care?", I'd say. After all, it appears to an incredible accuracy of 99.997% in GP and the number hadn't even been mentioned until the early sixteen hundreds. I thought that fact alone ought to get someone's attention. Well God bless Dr. John DeSalvo, the good people at GPGRA especially John Cadman and William Kapsaris and his 'Amazing Little Epsilon' email list. Finally, someone was listening.
e WANTS TO PLAY TOO!
There is a long standing assumption in Egyptology, and for good reason, that the numbers Pi(π) and Phi(φ) (you know Phi [(SQRT 5)+1]/2, of Golden Ratio fame) while appearing to remarkably high degrees of accuracy in GP, were in fact no accident but intentional by design. But as I will show, so too does the number e appear as a ratio in GP, and in fact, by way of the simple identity;
β/θ = e/2
e actually noses out Pi by a hair (and given the sheer size of the Great Pyramid a hairs width is not all that much of an exaggeration).
Let me show just how close the Pi and e proportions are by way of example;
Look at the clock face in (fig.1) and focus on the first minute after 12. That little minute section is 6 degrees of the overall 360 degree circle. Now, in your mind or better yet on a sketchpad, section off the minute into 6 equally spaced units... got it? Choose just one of those 6 units and now you're looking at 1 degree of arc. Now take that 1 degree slice and divide it into 60 equally spaced slivers, pretty small aren't they? In terms of angles those are called minutes of arc. Wait! I'm not done yet. Now stretch your imagination a bit further or get a bigger piece of paper and divide one of those itsy bitsy slivers into 60 more even tinier pieces... those are called seconds of arc (not to confuse arc minutes and seconds with the time units of the same name). So as you can imagine 1 second of arc is a very, very tiny unit. On this scale then, a Pi and e proportioned pyramid would differ by only about 12.5 seconds of arc! And since there are 3,600 seconds of arc in 1 degree this puts the Pi and e proportions' respective difference at one part in 1,737 over the spatial area of one minute of (time) on your wall clock!!! Now that's close!
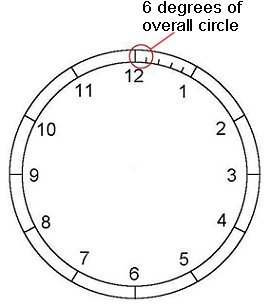
(fig.1)
The Pi proportion has the unique identity of the height of a right triangle being taken as 4 times the multiplier of Pi in the base as in the approximate GP triangle measured in royal cubits in (fig.2):
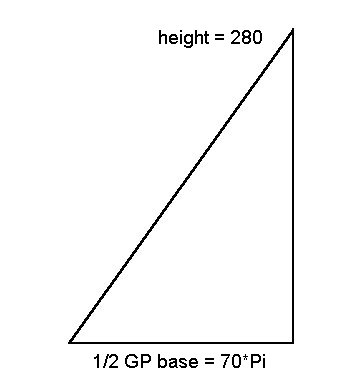
(fig.2)
Whereas upon reducing the fraction:
(70*4)/(70*π) or 280/(70*π)
You are left with the convenient identity:
4/π
So for any size triangle with this base-to-height relationship the triangle is said to have 'the Pi proportion'. This identity consequently, gives any pyramid with this relationship a Pi proportion. It just so happens that the Great Pyramid fits quite nicely into both the Pi and e formulae, in fact to 99.993% and 99.997% respectively. With the Great Pyramid being so very close in ratio to both of these models, it causes one to pause and wonder at the chance of such an occurrence being accidental as opposed to mere chance. After all, if you're going to immortalize some numbers for all of eternity in such a Grand undertaking as the Great Pyramid (to make no mention of purposes relating to shape effect, etc.), I can think of no better numbers than Pi, Phi, and e to bestow that honor upon.
* Pi for its geometry
* Phi for its aesthetic beauty
* And e for its inherent growth properties
The nice thing about the Pi and e proportions is that they exist as pyramids in their own right and can be examined without ever making reference to the Great Pyramid at Giza. I say that again; the Pi and e proportions exist independent of the Great Pyramid! But as it happens and happily so, the Great Pyramid conforms almost perfectly to either one of these models. And as I stated earlier and which you'll see in a moment, the e pyramid angles are actually a bit closer (albeit by a hair) to the observed GP angles than are the Pi angles. Don't believe me? Let's look at the data.
COMPARING RATIOS
The following GP dimensions are from W.F. Petrie as per this website under 'general articles/general information articles/measurements of the Great Pyramid' and are generally accepted as the standard GP measurements. I now invite everyone to follow the numbers and come to the same conclusion.
NOTE: In my calculations I have ignored the slight concavity issue as witnessed down the centers of all four slope of the Great Pyramid. That is a very important fact to leave out, I know, but for the primary purpose of comparisons of 'general pyramidal' shapes namely of the Pi and e proportions the reader will forgive me. I intend to investigate the concavity issue as soon as I can.
Great Pyramids External Dimensions:
Height = 280
Lengths of sides:
North = 439.67
South = 440.05
East = 439.93
West = 439.87
Since the length of sides vary slightly I took their average:
(439.67 + 440.05 + 439.93 + 439.87) / 4 = 439.88 average side
and taking the height at 280 and a little trigonometry the primary angle beta(β) works out to:
51° 51' 01.32" (see fig.3)
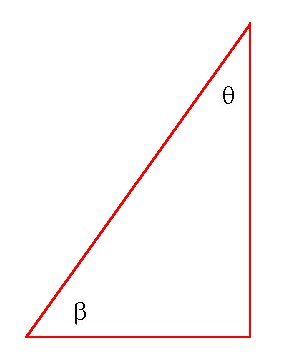
β = 51° 51' 01.32"
(fig.3)
This now being the basis for the comparisons that follow, I list here four other ratios in descending order of proximity to the above stated GP shape, and again I encourage the reader to do the math for yourself if you be so inclined.

So, as you can easily see, the e proportion slightly edges out the Pi proportion by just a few seconds of arc or more precisely: 12.43" in actual proximity to GP!
FINALLY, DOING THE e MATH
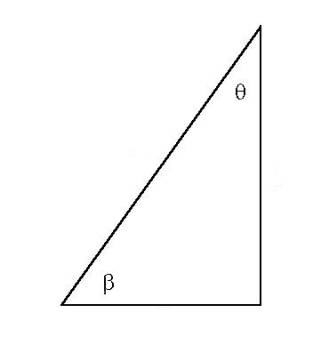
What follows is some algebra based on the above triangle and given the initial assumption:
β/θ = e/2




SUMMING UP

I note here that all four of these ratios are extremely close to the actual ratio present in the Great Pyramid with e and Pi being exceedingly close.
In closing I must say that I don't know for certain what purpose the Ancients had intended for this marvelous structure, but what I do know and what seems abundantly clear is that e is fixed into the angles to an incredibly high degree of accuracy, even by today's standards, and closer even than Pi! Further, if the 'e' model I present here were used to build a pyramid side by side to GP then, (barring the slight concavity of sides, added capstone, weathered blocks, and lack of an outer casing) they would be INDISTINGUISHABLE from one another without the use of sophisticated surveying equipment! The same too can be said of the Phi and 'Little Epsilon' pyramids whose 1 minute and 2.5 minutes of arc, respectively, are still more accurate than anyone could ever hope to achieve on such a Grand scale.
And remember, you can factor out the Great Pyramid completely with regards to both the e and Pi proportion and approach this purely as a simple 'generalized' pyramid problem and what you end up with is the shape of the Great Pyramid at Giza.
Questions and Comments
(especially if you have seen this 'e' ratio anywhere) to:
Rick Howard email: thunddd@attbi.com
Copyright 2002