ABSTRACT:
Had the Great Pyramid at Giza never been built, the discovery of the perfect
inter-relationships of three independent right triangles presented here would be
more of a mathematical curiosity than a theory. The TTT reveals a perplexing
synchronicity with its three specialized triangles if only to marvel at
their enigmatic and nearly identical shapes. It is a conundrum however – in
the sense that without the Great Pyramid's very existence we likely would never
have found all three of these triangular shapes not to mention relating them one
to the other. That said, my postulate concerning three fundamentally unique and
nearly congruent right triangles as being quintessential of three independent
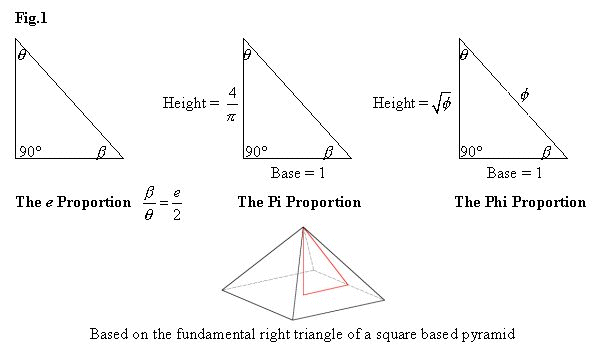
theoretical models of the Great Pyramid (Fig.1),
is that the resultant ratios when interlocked in a specific mathematical way
tend toward an optimally shaped triangle… that triangle in fact being the
fundamental right triangle of the Great Pyramid at Giza. Specifically it can be shown that the integer
‘2’ in the denominator on the right hand side of the e Proportion
causes the shape of the e triangle to resemble extremely closely, that of
both the Pi and Phi triangles. Indeed the problem can be modeled like this: Find
an integer that when divided into e results in the nearest (beta/theta)
angle ratio to that of the Pi and Phi angular ratios of same. No
other integer than ‘2’ comes even remotely close to affecting the desired
shape. Far and away closer to the Pi and Phi triangles than a denominator
consisting of either of the consecutive integers ‘1’ and ‘3’, the number
‘2’ in fact causes the e triangle to be so close to the averaged
angles of the Great Pyramid as to be accurate to within two
ten thousandths of one degree! It will be shown that the TTT leads to
a baffling equation with the least possible number of terms such as to result in
the Golden Ratio Phi 
as one of only a few real
number solutions.
If this isn’t strange enough it turns out that the theta angle of the e-proportioned triangle is one of two possible acute angle solutions in a generalized mathematical problem with the other solution being the tetrahedral angle of 60-degrees (See Section III - Fig.2 - Solution 2). This is curious considering the relatively new field of hyper-dimensional physics as expounded by the founder of the Enterprise Mission group - Richard C. Hoagland in his book The Monuments of Mars: A City on the Edge of Forever 1. The 60-degree tetrahedral angle – from the equilateral triangle – figures prominently in Hoaglands theory of the hyper-dimensional geometry present at the Cydonia region on Mars. In the computational tables contained in his book and with regards to my own findings here, I am not too surprised that in addition to the tetrahedral angle reference in the TTT that the number e is redundant at Cydonia. I would be lying to say that I’m not excited to see the Great Pyramid's hidden mathematical message correlate so closely to the Enterprise Missions research into the Martian structures. Monuments is a thorough study with far reaching implications and should be read by the serious investigator and inquisitor into our enigmatic remote past. The TTT offers a fairly compelling argument for the design of the Great Pyramid as having been ‘handed down’ from an earlier epoch and tends to support the Egyptian (Khemitian)2 / Cydonia hypothesis along with the many other various Earth/Mars correlations in the ancient world.
SECTION I. MAIN PAPER:
My goal in this paper is not so much to herald my belief in an ancient high-tech society as to delineate a mathematical model of the three triangles here considered. I will expand on the not-so obvious connections buried within these three astonishing shapes to the discovery of the numerically perfect relationships I found by cross-referencing identities and substituting terms in the equations. The impetus for the TTT is a newly discovered ratio I was lucky enough to stumble upon while examining the Pi – Phi Proportions. By convention then it seemed fitting to refer to the new ratio as the e Proportion*. In Section II of this paper I outline the mathematical derivation of this ratio but stated simply; the e Proportion is the ratio of acute angles (beta and theta) for the specific right triangle as shown in Fig.1. For reasons I can’t fathom, this ratio has eluded historians and researchers alike for all the years since the Pyramid's were built and this in itself is something of a mystery considering all the mathematical analysis’ focused on this megalithic enigma. Had the presence of e (often called the Euler number) in the angles of the Great Pyramid been less pronounced one could forgive researchers past and present for the blatant oversight. But this is not the case since to find the number e (2.71828…) in its shape is no more difficult than to find the linear based ratios of Pi and Phi.
I believe the appearance of e in the Pyramid, by virtue of the TTT's final equation, will add depth to the Pi – Phi debate and even challenge if not forever change our long held notions of a Pi – Phi based theory of the design. The e Proportion was the missing piece of a cosmic puzzle that would link the Pi and Phi triangles together and unexpectedly lead to the creation of the present theory. The TTT is in fact the natural evolution of the discovery of the three triangles here examined, and though interesting in it’s own right, the e Proportion was only the necessary precursor to something more profound.
* My article The e Proportion: The Euler Number and the Great Pyramid, Great Pyramid of Giza Research Association (GPGRA), Research Articles section, gizapyramid.com – Director, John DeSalvo, Ph.D
Having the number e (to an extremely high approximation) appear suddenly while examining the angles of the Pi triangle, I couldn’t help but be awed by the synchronicity of the constants. Seeing how unfathomably close these two triangles were to each other I set about looking for answers. How remotely improbable it seemed were these triangular shapes to be so close together. Was it mere coincidence? Could there be a connection to the numbers e, Pi and Phi that had simply been overlooked for all these many centuries? These were some of the thoughts that drove me initially. These questions coupled with the ongoing search for the Great Pyramid's elusive design ratio drove me further down the path. The design ratio being still under debate by many researchers has left those on the quest in a state of bewilderment. And though I’m not sure that what I’ve found is that coveted ratio, on the other hand I’m not sure it isn’t either. The TTT though mathematically sound, will probably not appeal to every esoteric Egyptologist in search of those elusory design angles; it should however be cause for very serious thought and consideration as to just what its ensuing equation means. I would be truly surprised to find that what has emerged from these triangles is not in some way indicative of that still so sought after design ratio of the Pyramid. The angles of the Great Pyramid seem oddly familiar to many people who study its shape and that fact does nothing to lessen the mysterious and overpowering influence the triangular giant has upon us. Its ratio truly is thought by some to be the holy grail of Pyramid-ology. I don’t presume to have captured the grail but I feel certain I’m in its vicinity.
All that being said, I state here my supposition that the Great Pyramid's ratio is quite possibly not one ratio but a set of three ratios inexorably tied together by the non-dimensionality of the e Proportion. It is my hope that from this point forward the Pi - Phi debate should not linger on indefinitely, but find comfort in that they are probably both correct. The e Proportion is not in competition with its two siblings, it is an equal partner. The perpetual Pi – Phi debate that I often refer to is akin to having a bubble in a rug. You push it under the furniture to hide it or you smooth it out by distributing it over a larger area but no matter what you do, no matter how you’ve managed to hide it you still know it’s there and it bothers you to no end. That is essentially my take on the on-going competitive nature of this debate where when one is taken as true, the other becomes an approximation – thus never the two shall meet. With bold and confident resolve the TTT has pulled up the carpet, re-cut it to fit the room and re-laid it to remove the bubble permanently.
One more note in the preface; I've
been criticized in my research leading up to this paper for developing a
contrived and predefined set of parameters used to support my postulate that the
numbers here mentioned are in some way predisposed to the shape of the Great
Pyramid. Let me be very clear in my address to this concern; the e, Pi
and Phi triangular models considered here, are theoretical models that conform
extraordinarily closely to the observed measurements of the Great Pyramid. The
Great Pyramid does not perfectly ‘fit’ into any one of these models but is
as close a fit as one could ever hope to find. My theory insomuch as it details
three independent triangles can only be called a theory in that it alludes to a
possible connection to the Great Pyramid. However, the equations for the three
triangles are not so much theory as they are fact. My inclusion of the Great
Pyramid into the TTT is based solely on the evidence of the empirical data of its
angular measurements being accurate to the theoretical models to within
two ten thousandths of a degree. The Pyramid of Khufu seems to beg us to
uncover the perfect union it keeps hidden in its internal composition.
Mathematically, the TTT’s final equation is irrefutable. The
discovery of the e proportion 
, as a dimensionless
component essential to this multi-proportional puzzle is the glue that binds
this theory together. Hence the e Proportion must
not be ignored lest one ignores the Pi and Phi ratios. The
perplexing sets of relationships hidden within these triangles are central to
this discussion, with results no less mysterious than one of its employed
equations – what some have called “the Euler equation of mystery”
.
The TTT is simple but requires some effort of associative thinking to fully appreciate. It is not a big or impossibly difficult theory to understand and one only needs an afternoon’s refresher course in basic algebra and trigonometry to see it through to the end. The focus of the present research is to show the interdependence of three nearly congruent right triangles whose proportionalities when viewed in a mathematically specific manner bring into question the notion of the Great Pyramid's shape as being mere coincidence. The result of my investigation, lends support to the Pyramid as a true mathematical anomaly. Uncertain as we are as to its ultimate purpose and symbolism it is clear beyond a shadow of doubt that there is indeed something very peculiar about the design shape of the Great Pyramid. In addition to offering us knowledge of the existence of these three unique triangular shapes, and in a somewhat more abstract mathematical sense, the Great Pyramid undeniably hints at a hyper-dimensional aspect as evidenced in the 60-degree solution to Eq.5.2. The TTT does not pretend to be some ultimate proof for there having been civilizations in our remote past capable of higher mathematics and technology, but by that same token however, the admittedly exquisite mathematical connections incorporated in the TTT are cause for very serious contemplation of such conjecture. The lack of archeological evidence that the ancient Khemitians had any system of what we would call ‘higher mathematics’ does not preclude them having the knowledge to design and build Pyramids. But the mathematical elements hidden away in the very shape of the Great Pyramid (in particular) are so pervasive as to render any argument of the design being mere coincidence – uninformed and absurd.
Critics will undoubtedly say that it is dangerous to jump to the conclusion of a high society that antecedes recorded history, and in defense of this I would counter; it is equally dangerous indeed foolish to be so arrogant as to ignore the obvious mathematical anomalies present in the ancient world. To their credit the ancient Khemitians were in fact quite sophisticated in their use of numbers and are known to have had an understanding of the concept of Pi and the Golden Ratio. The serendipitous presence of e in the mix however is immensely interesting and difficult to reconcile and has led me to the realization that if one desired to design a mathematically mysterious pyramid one couldn’t possibly find a shape more meaningful than the very shape we see at Giza. The presence of e in the Pyramid is at best an enigma that requires further investigation.
I don’t believe that the people of ancient Khemit were aware of the number e. The very history of this little power-house of a number bares this out. First hinted at in the early seventeenth century, the Euler number (to paraphrase Eli Maor in his book e: The Story of a Number)3 – “probably arose from the mundane study of compound interest”. The problem of compound interest was a distinctly seventeenth century mathematical challenge that facilitated widespread commerce and economic growth that eventually led to the Industrial Revolution. If the number had been known prior to that time in history, societies of the past would have been profoundly impacted with financial growth and the advent of the Industrial Revolution would undoubtedly have come much earlier. Clearly then, this number couldn’t have been known to the ancient Khemitians lest it would surly have been documented – as the Khemitians were meticulous record keepers.
Being the base of natural logarithms, e is actually more present as a ratio of angles in the Great Pyramid than is Pi or Phi with their linear dimensions. Using William Flinders Petrie’s4 established standards of the Pyramid’s measurements it is well to note that the standing Pyramid at Giza when it’s dimensions are averaged - more closely approximates the e Proportion than a perfect Pi Proportion (albeit by only a few seconds of arc). This is all the more curious considering Petrie used the ‘Pyramid Pi’ (22/7) in his calculations… more on the Pyramid Pi later.
The subtle similarities of angles in this theory are not trivial – they are in fact perfect to the overall picture. All we can say is that the brainchild of the TTT – its final equation – is true and beyond refute. We are at a loss to explain it. It is apparent that either by intuitive design or deliberate intention, the designer(s) of the Pyramid agreed upon the shape we see at Giza – it was a carefully thought out architectural decision. But setting aside any consideration of design intentions (as they are not applicable to the equations that follow), one thing the Pyramid offers, indeed communicates to all future generations are a set of axioms that slowly have led us from the discovery of one mathematical identity to another with still more waiting to be found. It is wonderful to find that a truly universal numerical statement exists in this ancient and timeless stone giant that relates the three constants e, Pi and Phi. This is a theory that inevitably would have come about over time and with respect to recent discoveries of pyramids being found off distant shores deep in the Atlantic Ocean, there is a growing body of evidence of there having been in the remote past an ‘Age of Pyramids’. In this way the arrival of the TTT seems timely.
The e Proportion leads to the TTT:
Having
identified a hint of the inconspicuous Euler number embedded in the acute angles
of the Great Pyramid, I generalized the problem and solved the angles for a
theoretically modeled e-proportioned triangle. The solutions for the
resulting beta and theta angles in hand I then went about
comparing them with the well established Pi and Phi triangles. I was struck at
first by how remarkably similar these triangles were to one another; they are in
fact all very nearly congruent. But close as they are one to the other, they are
all slightly different nonetheless. Knowing the equation
for the Golden Ratio: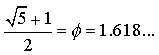 
,
and Leonhard Euler’s famous equation
, I was curious as to what might happen if I were to substitute the term '1' in
the equations. What followed were subsequent progressions in the substituting of
terms involving the three triangles. By incorporating the e Proportion into the Pi
and Phi Proportions, a mathematically perfect balance is shown to exist. To
understand this delicate balance one must remember that the angular systems of
measure in degrees and radians are related by the conversion formula: 
. There are absolutely no approximations of
the constants involved in the derivation of the TTT. The three numbers are
perfectly represented and this is made all the stranger considering that the
three triangles are based on three transcendental numbers e.g. numbers with
non-terminating infinitely expanding decimals. With a little algebra their
resultant right triangles are perfectly equated to the integer ‘1’, and by
this the transcendental decimal expansions seem less superfluous than
profound. Truly, one has cause to stop and contemplate
the meaning and beauty of the design.
A question worth asking is “How can three slightly differing right triangles be shown to have perfect co-relations to one another?” The presumption seems to defy logic. Considering that any number of equations of unity can be created if the denominator ‘2’ in the e Proportion were changed to some arbitrary number, what you lose in the trade is the very ‘shape’ of the triangle! Put another way; given the stipulation that the denominator in the e Proportion must be an integer value, then the Pi and Phi triangles closely approximate the shape of the e triangle if and only if that integer is 2. This is cause for thought as to the strange simplicity at work in this particular arrangement of triangles. The Great Pyramid happens to be so close to any one of them that from a designers point of view, they could have chosen any one of the three models for its design - and more amazing is the fact that had they chosen upon any one of the three models, the TTT would still have eventually been discovered – that is how close the ratios are one to the other. That stated, it is not my intention to give favor to one design model over another; in fact quite the contrary. This is a theory that fully embodies the three ratios and to change one number in any of their three decimal expansions respectively, would throw the whole thing into a universe of purely imaginary numbers with no real number solutions whatsoever, hence there could be no Triple-Triangle-Theory.
A note on the Pyramid Pi ratio:
The so-called Pyramid Pi ratio (not considered in the TTT and not to be confused with the Pi ‘proportioned’ Pyramid) simply stated is an additional pyramid model that presumes a value of Pi as a fraction of integers; (22/7). The Pyramid Pi model is virtually the Pi Proportion in Eq.1.2 however instead of the true value for Pi the value (22/7) is employed. This fraction of integers yields convenient integer dimensions of 440 and 280 royal cubits for the base and height, respectively, of the Great Pyramid. Purely on its own merits this ratio too would give birth to the study of the three triangular models and the TTT and in fact might be the very approximation the ancients would have used for Pi if indeed Pi had been employed by the designers. I emphasize here that the architectural design ratio of the Great Pyramid notwithstanding, the empirical measurements of the Pyramid are of secondary concern as applies the TTT, - my research has less to do with physical measurements and preferred ratios than with pure mathematical inquiry.
One could imagine the Pyramid Pi having been employed by the ancients if for no other reason than to utilize its resulting integer lengths to facilitate a practical construction model for the builders. This in no way deters from there having been a plausible architectural design model with a more mathematically sacred purpose. I view the Pyramid Pi’s ratio and its resulting even dimensions as another splendid display of universal synchronicity. Considering the overall strange aspects of this theory I am inclined to view the Pyramid Pi ratio as being connected to some higher aspect of dimensionality. Through its simple arithmetic, its ratio seems to lead us down the path to the eventual formation of a specific pyramidal shape. From a builder’s perspective, the perfect Pi ratio is not only impractical it is meaningless. Any representation of Pi would by necessity be an approximation. The (22/7) ratio is a very close and practical value for building purposes and could almost be said to be a sort of ‘universal approximation’ for Pi. In addition to W.F. Petrie’s use of this ratio, the Pyramid Pi also appears in the works of various other researchers such as Joseph Turbeville’s important contributions of Fibonacci based number tables in his book A Glimmer of Light From the Eye of a Giant 5, where his use of the Pyramid Pi blends in naturally with his Fibonacci number tables – again more evidence of the Pyramid Pi’s universal applications. Could the integer fraction (22/7) be nudging us along to probe the deeper mysteries in a mathematically complex yet pragmatic universe? In this way I appreciate the Pyramid Pi and in no way do I feel amiss in the non-inclusion of this triangular model in the TTT. The theory I present here requires that the mathematical constants be true – not approximations, and as will be evident in the following analysis any approximations for the constants e and Pi would in fact result in an imaginary number output.
Let me be clear on one point; the TTT is not about perfect physical measurements of the Great Pyramid. It is about the subtle relationships of e, Pi and Phi in three triangular models. In fact because of the inarguably pervading balance present in the TTT, physical shortcomings to the theoretical models are incidental. Such arguments that would profess having one ratio more meaningful than another due to this or that measurement of the Pyramid seem now forever more trivial than evidential. Should we embrace every theory that comes along? Certainly not. But when theory combined with sound mathematical reasoning seems to say something about the world, it would be unfortunate to summarily dismiss such analysis out of hand. As John Cadman creator of the Hydraulic Pulse Generator Theory* states in reference to the e Proportion “He who solves this puzzle will have to take all of the factors into consideration, including shape effect. The shape is an energy lens which utilizes e for exponential energy growth”.
* John Cadman’s remarkable Hydraulic Pulse Generator Theory, and his working model, Great Pyramid of Giza Research Association (GPGRA), Research Articles section, gizapyramid.com – Director, John DeSalvo, Ph.D
SECTION II. THE e PROPORTION:
Given a right triangle :
with an assumed ratio :
And knowing there are 180-degrees in a triangle, we solve for the angles beta and theta using degrees for easy visualization.
Solving for angle beta and knowing
the sum of angles for a triangle is 180-degrees we have : 
So it follows : 
Substituting theta into
we have :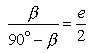 
Reciprocating both sides :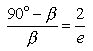 
Simplifying :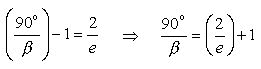 
Reciprocating both sides again :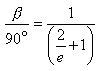 
Multiplying both sides by 90 :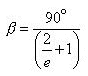 
Factoring 1/e out of the denominator and simplifying :
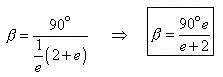
Solving now for angle theta
The assumed ratio :
From the triangular identity :
so it follows :
Substituting beta into
we have : 
Simplifying : 
Reciprocating both sides :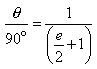 
Multiplying both sides by 90 :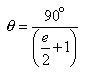 
Factoring 1/2 out of the denominator and simplifying :
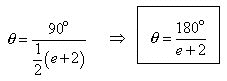
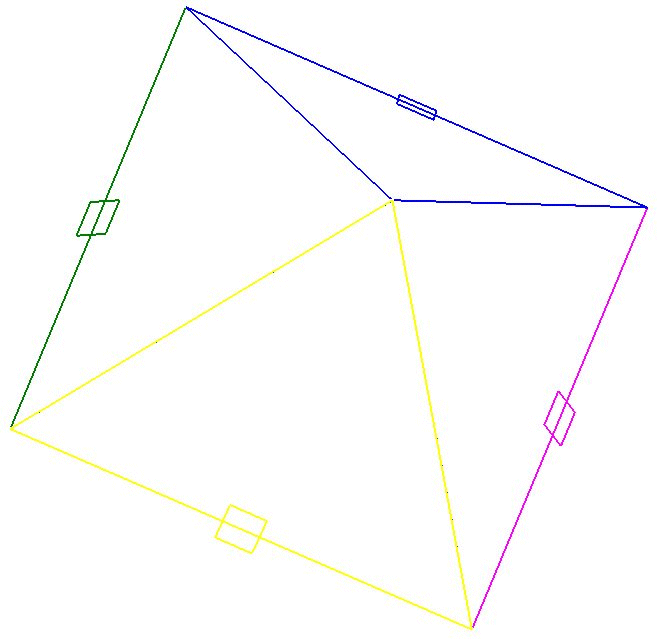
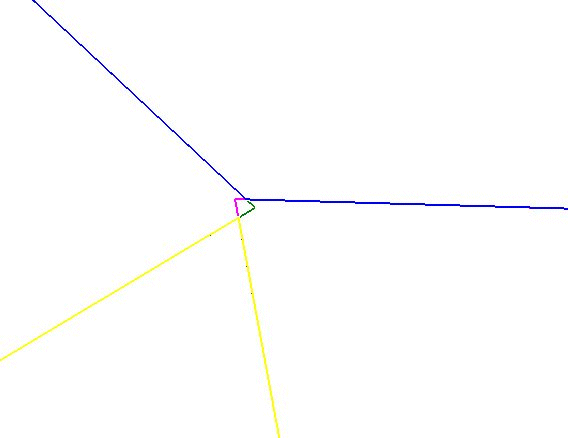
Shown above is a computer pyramid model with a square base. In each quadrant the three independent triangular models; e, Pi and Phi are represented with the addition of the Pyramid Pi as the fourth side. The image on the left is a top-down view with the image on the right showing an extreme close up at the apex. Here we can begin to see the misalignment in the geometry, but only at very high magnification. Modeled by Tim Alison
What follows is the main purpose of this paper; the Triple-Triangle-Theory...
SECTION III. THE TRIPLE-TRIANGLE-THEORY:
1.0
Given the three specific triangular ratios for e, Pi and Phi respectively, we here examine their inter-dependencies in the TTT. We let all bases equal 1. Subscripts for
and 
indicate the representative triangle. Note that it would be simpler to work the
problem in radians from the start, however I have chosen to begin in degrees so
as to illustrate to readers not as familiar in the system of radians the
difference of Pi as an angle as opposed to Pi as a component of length.
(1.1)
The e Proportion: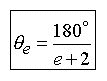
A dimensionless
ratio of angles from the identity :
(1.2)
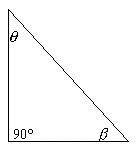
The Pi Proportion: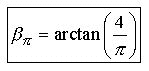
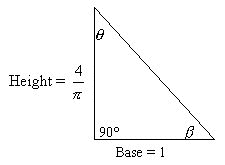A dimensional
ratio of known side lengths where angles are linear dependant.
(1.3)
The Phi Proportion: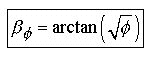
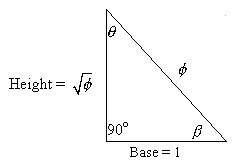A dimensional
ratio of known side lengths where angles are linear dependant.
2.0 Now we consider the identities of the two following equations; the Golden Ratio and Leonhard Euler’s famous equation relating e, i and Pi to -1 :
(2.1)
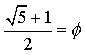
(2.2)
Note:
( in mathematics i is
called the imaginary unit )
3.0 We combine Eq.2.2 into Eq.2.1 by substitution :
(3.1)
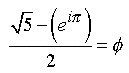
4.0 We now re-write the e Proportion Eq.1.1 in terms of e :
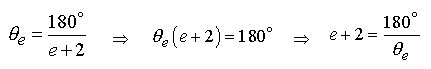
(4.1)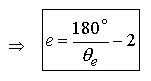 
Remember
that in Eq.1.1, 
and 
are degree angles whereas ( e
and 2 ) are constants.
5.0 Taking Eq.3.1 we substitute e for the re-written e Proportion Eq.4.1 (Remembering that the expression inside the parenthesis must equal e in order that the equation is true) :
(5.1)
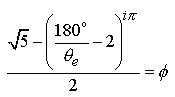
At
this point we can examine the effect the imaginary unit
i has on Eq.5.1. Again,
we know that the expression inside the parenthesis
must equal e
exactly for the statement to be true. So
now thinking in general terms we can set
and
as unknown variables
and 
respectively
:
(5.2)
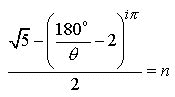
Now
we ask a question; “Find a real acute angle
(in degrees)
such that
is real”. Since there are only a few sets of real number
solutions, we list all 
values in Fig.2. In
doing so we avoid the imaginary number domain.
Fig. 2
Shown here are the four
angle solutions such as to output a real number. Note: 
as an angle solution is omitted as it is an imaginary number with
infinite real number outputs.
Solution 1
Solution 2
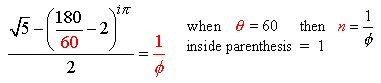
Solution 3
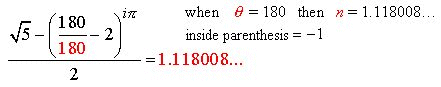
Solution 4
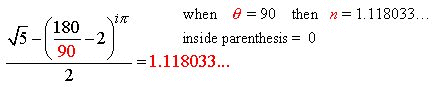
This situation can be generalized as follows: (When a = 2 then Eq.5.3 describes the e Proportion)
(5.3) 
Following
is an even more generalized formula of Eq. 5.1 where
.
Note that when Eq. 5.3 is solved for
becomes
a.k.a.
(the e Proportion) therefore causing the output
of
Eq. 5.4 to be the Golden Ratio
.
(5.4)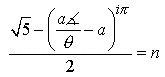 
In
Eq. 5.4
is a
real number if and only if 
equals; 
(where the exponent x is any real number). Any other value inside
the parenthesis other than these five values would cause
to
be imaginary.
outputs when a
= 2, provides us with a unique relationship for the respective
values when is made to equal; (e
or 1).
This in essence ties the
angle e.g. (e-proportioned
angle) to the tetrahedral
60-degree angle! We see in Fig.2 (Solutions 1 and 2), that
and 60-degrees, respectively, cause the equation to reciprocate the Golden Ratio
which is the only number in all of mathematics with this intriguing fractal
aspect (that is precisely why it’s called Golden).
After examining in Fig.2 all possible solutions for Eq.5.2 that satisfy the
conditions of our question, we realize that given any other values for the
unknowns 
, other than Solution 1; 
, that we would loose the e Proportion, that is to say - the very shape
of our e triangle. We therefore choose solution 1 and thereby maintain
the e Proportion in Eq.5.1 knowing that we are grounded safely in the
domain of real numbers. Indeed any variation of the terms inside the
parenthesis other than the solutions given in Fig.2 would be disproportionate to
e and would result in the output
as imaginary.
Satisfied insofar as the constants e and Phi retain proportionality, we
continue on.
6.0 Since the TTT deals specifically with the three universal constants e, Pi and Phi and we now know from the general Eq.5.2 that we have preserved the e Proportion and the Golden Ratio, we can now confidently continue on from Eq.5.1 and turn our attention to an interesting and important term. We notice 180-degrees in the numerator of the expression inside the parenthesis :
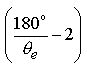
We realize at this point it would be convenient to convert from degrees to radians since :
Using
the conversion formula
we convert 180-degrees and to radians.
Eq.5.1 now becomes :
(6.1)
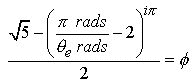
7.0 We now have Pi inside the parenthesis thus allowing us to substitute from the Pi Proportion in Eq.1.2
Note: We must now convert our thinking from degrees to radians so from here on all angles and trigonometric functions are in radians. Re-writing the Pi Proportion in terms of Pi we have :
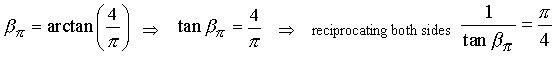
(7.1)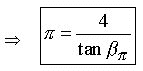 
Substituting now from the Pi Proportion into Eq.6.1 we have :
(7.2)
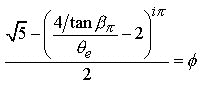
And simplifying:
(7.3)
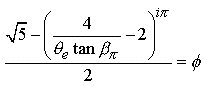
8.0
What has happened here is that in substituting
the Pi ratio into Eq.7.2, the Pi identity given in the Pi Proportion in terms of
the number
Pi
- being essentially dimensional - is made to replace
Pi radians, which is an angle and is associated with the
non-dimensionality of the e Proportion. It now becomes evident that the
conversion from degrees to radians is the thread that ties the dimensional to
the non-dimensional aspects of the TTT. In other words by converting 180-degrees
to Pi-radians inside the parenthesis, the 'linear' aspect of Pi (being a ratio
of two known lengths; 
from the Pi Proportion) is now tied to the e
Proportion angle
which comes from a 'dimension-less' identity. So we see inside the parenthesis of
Eq.7.3 that
:
The perplexing and serendipitous interchange between the dimensional and non-dimensional components of these equations leads us now to a strange yet beautiful final result.
9.0
All that is left to do now to complete the perfect
inter-relationships of the three triangles
are to relate them to the Golden Ratio
We
re-write the Phi Proportion Eq.1.3 in terms of
:
(9.1)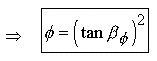 
Now substituting Eq.9.1 into Eq.7.3 we have :
(9.2)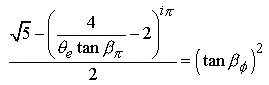 
Taking the square root of both sides :
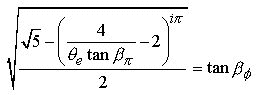
Taking the arctan of both sides :
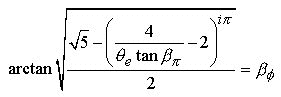
And
finally, dividing both sides by 
we
have the completed TTT equation of unity where all three triangles are perfectly
represented :
(9.3)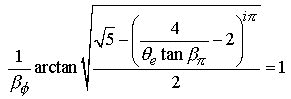 
Note that Eq.9.3 could also be written in terms of all beta or all theta angles, but that the present form of two beta’s and one theta help lend the equation to it’s simplest form.
In Conclusion:
One person that investigated the derivation of the TTT commented that “there’s nothing odd about it” until I remind him of Eq.5.2 where we learn that by keeping all relationships proportional, the domain of imaginary numbers limits us to an optimal triangular formation where he then retracted his statement. We see how the three triangles seem to zero in on a specific shape and being well within the range of our modern day building tolerances that shape is, for all applied purposes, the fundamental triangle of the Great Pyramid at Giza.
In the physical world it is impossible to calibrate with perfect accuracy, measurements that contain irrational numbers. The Great Pyramid having less than two ten thousandths of one degree conformity to the e Proportion and a tiny bit less for the Pi and Phi triangles, is by the very nature of our physical universe a mathematically imperfect shape. However, through it’s hidden ratios it seems to point us to the realm of the real numbers domain. By its very existence it is positioned an imperceptible distance from the fulcrum of a mathematical balance; on one side teeters the domain of the real numbers and on the other the imaginary. Due to the inherent imperfections of measurements in our physical world and by the very properties of irrational numbers and the imaginary number element in the equations, the Great Pyramid is resigned to tip the scale ever so slightly to the imaginary side. Serendipitous harmony has never been so exquisite. One may even philosophically muse that our empirical universe resides in an imaginary domain whereas Eq.9.3 shows that in theory perfection only exists in the realm of the real. We are forced to conclude that the three constants here mentioned and just as perplexingly, the three nearly congruent triangular models they represent are forever intimately linked via the Triple-Triangle-Theory.
Deliberate or not, the surreal harmony of the TTT is intensely peculiar and one thing appears certain; the ancient Khemitians didn’t possess the mathematical skills to pull off such a splendid union of ratios. How this design came to be remains a mystery but should inspire us to keep an open mind as we investigate into the remote past. The TTT should add new light to the ongoing Pi – Phi debate and press us ever harder to find answers to this most deserved of the Seven Wonders of the ancient world. Without a single inscription of reference, the ineffable Great Pyramid stands as a repository of meaningful numbers. As surely as the angles of an e-proportioned triangle and the linear dimensions of a Pi-proportioned triangle can be adjusted proportionally to compliment one another, the real number output of Phi in the equations keep the shapes confined to the mathematical identities we see here. We are likely drawn intuitively to the creation of physical representations of perfection as evidenced by the aesthetic presence of the Golden Ratio subtly hidden in the shape of the Pyramid. Truly there can be no better suited home than the immortal Great Pyramid to eternalize such a pristine mathematical balance. To my mind the commonalities of the triangles are circumstantial, for whether the ratios were deliberate or not the Great Pyramid stands before us with its angles fixed. From this point forward one cannot argue that the shape of the Great Pyramid is not universal in design… for it surely is.
REFERENCES
[1] Hoagland, Richard C. The Monuments of Mars: City on the Edge of Forever, North Atlantic Books, Fourth Edition (1996) ISBN 1-883319-30-7
[2] Mehler, Stephen S. The Land of Osiris, page 41, Khemit; the original name for Egypt meaning “The Black Land” based on Pre-Greek indigenous teachings, Adventures Unlimited Press (2001) ISBN 0-932813-58-5
[3] Maor, Eli e The Story of a Number, page 23, Princeton University Press (1994) ISBN 0-691-03390-0
[4] Tompkins, Peter Secrets of the Great Pyramid, page 106,Harper & Row Publishers(1971) Standard Book Number: 06-014327-4
[5] Turbeville, Joseph A Glimmer of Light from the Eye of a Giant, page 5, Trafford Publishing (2000) ISBN 1-55212-401-0
* * * * * * * * * *
Special thanks to my trusted friend and mathematical advisor Tim Alison, for listening to my endless Pyramid babble while checking my math, constructing the computer model and generally keeping my feet on the ground.
Copyright ©, 2003 Rick D. Howard
Questions and Comments:
thunddd@attbi.com
